Tactical Voting Basics

Research Hub

The Center for Election Science

–

Introduction

Tactical voting, also called strategic voting, is when voters cast an insincere ballot in order to increase their expected value for an election outcome. A common example of this behavior is when supporters of a minor party candidate vote for their favorite major party candidate, based on the impression that the minor party candidate is unlikely to win.

Plotting Tactical Vulnerability and Performance

In discussions of various alternative voting methods, it is often claimed that one voting method or another is “vulnerable” or “susceptible” to tactical voting. But such rhetoric is often misleading.

To illustrate that, consider the “Random Ballot” method, with which the election is decided based on a randomly chosen ballot. This has the academically interesting property that it makes a tactical vote equivalent to a sincere vote. That is, it is completely invulnerable to strategy. However, it is clearly an extremely undemocratic system.

To illustrate this concept, consider the following simple graph of hypothetical voting method performance (i.e. “democratic-ness”). The X axis represents the ratio of tactical voters. On the left, 100% of voters are sincere. On the right, 100% are tactical. The blue line for Random Ballot is flat, which demonstrates that its performance is unaffected by tactical voting. The red line is for a hypothetical “normal” voting method, whose vulnerability to strategy is apparent from its downward slope.

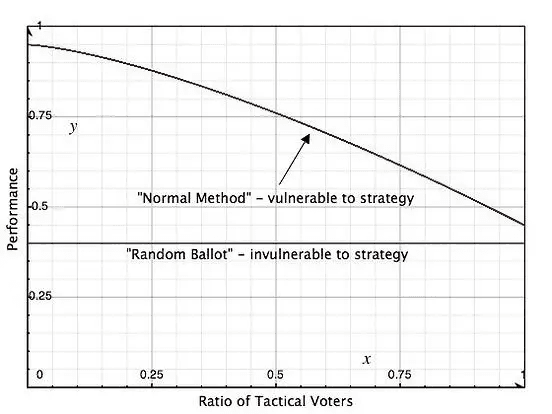
This graph reveals how misleading it would be to claim that Normal Method is more vulnerable to tactical voting than Random Ballot. In fact, Normal Method is better with 100% strategic voters than Random Ballot is with 100% sincere voters.

Simulating Tactical Voting

The above values were purely hypothetical, and only intended to convey a concept. However, real figures of voting method performance have been calculated for a host of voting methods, using a metric called “Bayesian regret“. The most extensive Bayesian regret calculations have been performed by a Princeton math PhD named Warren Smith. Sample figures are available here and here.

The following figure, taken from page 239 of William Poundstone’s book Gaming the Vote, expresses Bayesian regret visually for several common voting methods, as a function of the ratio of tactical voters. Score Voting here is referred to by its alias, “Range Voting”. Notice the marked improvement versus Instant Runoff Voting.

Voting Method Myths

Widespread misinformation persists about the relative merits of various alternative voting methods, with regard to tactical voting. We now discuss a few of those methods.

Instant Runoff Voting/Ranked Choice Voting

IRV is a ranked voting method. Proponents of IRV commonly claim that it is highly resistant to tactical behavior. Our extensive analysis finds quite the opposite. IRV fails the Favorite Betrayal Criterion, meaning it can punish voters for sincerely ranking their favorite candidate in first place. This incentivizes a type of exaggeration which causes it to degenerate approximately into ordinary Plurality Voting (aka First Past the Post). Moreover, naive voter exaggeration means that voters commonly utilize this strategy, without even being aware of the mathematical basis for it.

Condorcet Methods

Contrary to common misconception, Condorcet methods are indeed susceptible to strategy. Here is some mathematical analysis from Warren Smith, which explores the susceptibility of various Condorcet methods to the burial strategy. One particularly concerning pathology is the DH3 scenario, in which naive exaggeration results in the election of a candidate considered worst by as many as 100% of voters.

Score Voting & Approval Voting

Despite common intuition, Score Voting is extremely resistant to the effects of tactical voting. Unlike virtually all ordinal (“ranked”) voting methods, Score Voting satisfies the Favorite Betrayal Criterion, meaning voters can always safely give the maximum support to their sincere favorite candidates. The aforementioned Bayesian regret figures show that Score Voting outperforms all commonly proposed alternatives with any mixture of strategic or honest voters.

Moreover, two theorems attest to the relatively mild effect of tactical behavior under Score Voting:

Tactical Score Voting may be, in practice, more likely to elect a Condorcet winner (when one exists) than real Condorcet methods.

Score Voting maximizes the number of voters who are “pleasantly surprised” by the election outcome.